Introducción Lógica Categórica
Introducción: La lógica categórica nos viene de una manera sistemática desde la Grecia antigua en los trabajos de Aristóteles conocidos como El Órganon que contiene varios trabajos, entre ellos de las categorías, primeros y segundos analíticos y tópicos. Desde su primer libro este mismo nos comunica la intención de la obra explicando
“ a continuación distingamos que es una proposición y que [es] un termino y un racionamiento, y cual es el racionamiento perfecto y cual es el imperfecto, y después de eso en que consiste qué tal cosa este o no este en la totalidad de tal otra y a que llamamos predicar acerca de todos o acerca de ninguno.”
En esta próxima serie estaré presentando los principio de la lógica categórica que de esto resulto. Veamos juntos exactamente que es el razonamiento correcto y tratemos de mejor entender como podemos respaldar nuestros argumentos asegurando que son lógicamente validos y sólidos. Si estas aquí, pues no hay mas que decir, ya tienes algún un interés o necesidad para llegar a entender estas cosas, comencemos!
Terminología de la lógica categórica:
La proposición: un enunciado afirmativo o negativo acerca de algo. En la lógica categórica las proposiciones afirman algo sobre clases de cosas utilizando términos.
El Término: aquello en lo que se descompone la proposición, v.g.: el predicado (P) y aquello sobre lo que se predica, es decir, el sujeto (S) (De aquí en adelante representados por la letra mayúscula S y P).
La Copula: las palabras “es” y “no es” son conjugaciones del verbo ser y se utilizan para unir los términos en una proposición al igual que para afirmar o negar la inclusión de un termino en otro.
La Clase: se refriere al termino en una totalidad incluyendo o excluyendo a todos o unos de los miembros de un grupo S o P.
Las forma estándar de proposiciones categóricas: una de las cuatro formas estándar que relacionan dos clases usando los términos S y P.
Las cuatro formas son:
- Todo S es P (Forma A).
- Ningún S es P (Forma E).
- Algún S es P (Forma I).
- Algún S no es P (Forma O).
Es importante notar que existen dos interpretaciones de las proposiciones estándar: La tradicional y la moderna. La diferencia es simple pero significativa. La interpretación tradicional cuanta con el importe existencial. El importe existencial nos indica que las proposiciones universales pueden hablar de una clase que no tiene miembros. Esto resulta en validez provisional ya que es necesario verificar la existencia de los miembros de la clase en cuestión. El símbolo para esto concepto es una X dentro de un circulo: ⓧ
Este cursó tendrá enfoque en la interpretación moderna solamente comentando sobre la interpretación tradicional ocasionalmente.
Parte 1: Las Proposiciones
Las formas estándar de proposiciones categóricas tienen algunos propósitos que se hacen evidentes en su formulación. La Proposición es un enunciado afirmativo o negativo pero también universal o particular. Esto se refiere a la calidad y cantidad de una proposición. La cantidad nos indica si la proposición afirma algo sobre todos (o ninguno) de los miembros de la clase del sujeto. Si habla de todos o ninguno de los miembros, la proposición es universal. Al contrario si habla de por lo menos un miembro pero no todos, la cantidad es particular. La calidad se refiera a la negación o afirmación de la proposición en cuanto a la relación del sujeto al predicado. Es decir, la calidad nos indica si pertenece la cantidad del sujeto al predicado o no.
Analicemos cada proposición por si misma identificando sus respectivas cantidades y calidades.
Proposición A
Todo S es P - Universal - Afirmativa
La proposición enuncia que la clase entera del sujeto S pertenece a toda la clase del predicado P.
Llamamos la cantidad de la proposición UNIVERSAL cuando refriere a todos los miembros del termino del S como es el caso en la proposición A. Se puede interpretar de la siguiente manera: TODO si es S, es también es P.
Llamamos su calidad el fin de la proposición, ya sea de afirmar o de negar la inclusión de un termino en otro. En el case presente vemos que la proposición AFIRMA que TODO miembro del la clase S pertenece a la clase de cosas P. La calidad se determina por la copula. En la proposición A, la copula es afirmativa ya que es la palabra “es” y no ”no es”.
Proposición E
Ningún S es P - Universal - Negativa
La proposición enuncia que ni un miembro de la calase de sujetos S pertenece a la clase del predicado P.
Llamamos la cantidad de la proposición UNIVERSAL cuando refriere a todos los miembros de un termino como es el caso en la proposición E. NINGÚN S son P.
Llamamos su calidad el fin de la proposición, ya sea de afirmar o de negar la inclusión de un termino en otro. En el case presente vemos que la proposición NIEGA que TODO miembro del la clase S pertenece a la clase de cosas P. En este caso, la calidad se determina por la palabra ninguna. En la proposición E, la copula es afirmativa, “es,” pero la proposición se mantiene negativa.
Proposición I
Algún S es P - Particular - Afirmativa
La proposición enuncia que hay por lo menos un miembro de la clase de sujetos S que pertenece a la clase del predicado P.
Llamamos la cantidad de la proposición PARTICULAR cuando refriere a por lo menos un miembro de un termino como es el caso en la proposición I. ALGÚN S son P.
Llamamos su calidad el fin de la proposición, ya sea de afirmar o de negar la inclusión de un termino en otro. En el case presente vemos que la proposición AFIRMA que por lo menos UN miembro del la clase S pertenece a la clase de cosas P. En este caso, la calidad se determina por la copula. En la proposición I, la copula es afirmativa, “es”.
Proposición O
Algún S no es P - Particular - Negativa
La proposición enuncia que hay por lo menos un miembro de la clase de sujetos S que NO pertenece a la clase del predicado P.
Llamamos la cantidad de la proposición PARTICULAR cuando refriere a por lo menos un miembro de un termino como es el caso en la proposición O. ALGÚN S no es P.
Llamamos su calidad el fin de la proposición, ya sea de afirmar o de negar la inclusión de un termino en otro. En el case presente vemos que la proposición NIEGA que por lo menos UN miembro del la clase S pertenece a la clase de cosas P. En este caso, la calidad se determina por la copula. En la proposición O, la copula es negativa, “no es.”
Parte 2: Distributividad y El cuadro de oposición
Distributividad: Cuando todos los miembros representados por el termino son afectados por la proposición, ese termino se dice ser distribuido. En caso de lo contrario, el termino seria no-distribuido. Para simplificar el concepto, tomemos un ejemplo,
Todos los Sapos son Peligrosos.
Podemos ver que esta proposición toma la forma de proposición A. Para determinar si los términos son distribuidos nos preguntamos:
“¿estamos diciendo algo sobre todos los miembros de la clase Sapos?”
La respuesta es que si. Entonces el termino S, que representa a todos los miembros de la clase Sapo, es distribuido.
Y también
“¿estamos diciendo algo sobre todos los miembros de la clase cosas peligrosas?”
La respuesta es no, por que solamente enunciamos que si algo es Sapo es también Peligroso. Pero no dijimos nada sobre todo los miembros de la clase de cosas peligrosas.
Podríamos hacer esto con un ejemplo para cada proposición estándar pero seria mejor entender el significado y luego seguir dos simples reglas:
Los términos sujeto son distribuidos cuando las proposiciones son universal en su cantidad.
Y
los términos P que predican sobre el sujeto son distribuidos cuando la proposición es negativa en su calidad.
Verifiquemos estas reglas con otro ejemplo.
Ningún Sapo es Peligroso.
Esta proposición toma la forma de la proposición E. Recordemos que la proposición E es Universal y Negativa. Si utilizamos las reglas concluimos que ambos S y P son distribuidos. Verifiquémoslo…
¿Se dice algo de todos los sapos?
Si. S es distribuido.
Y
¿Se dice algo de todas las cosas Peligrosas? Si. P es distribuido.
Conclusión: si ni un sapo es peligroso, podemos deducir que ni una cosa peligrosa es sapo.
Términos Importantes
Juicios opuestos: proposiciones que comparten términos pero no calidad y/o cantidad.
Contradictorios: proposiciones que se niegan entre sí. Es decir, difieren en calidad y cantidad. Si una es verdad la otra será falso. No pueden ser ambas verdad ni falso al mismo tiempo.
Contrarios: dos proposiciones que no pueden ser ambas verdaderas al mismo tiempo pero si ambas falsas. (A & E)
Subcontrarios: dos proposiciones que pueden ser ambos verdad pero no ambos falsos. (I & O)
La relación entre las cuatro proposiciones se pueden visualizar usando un cuadro.
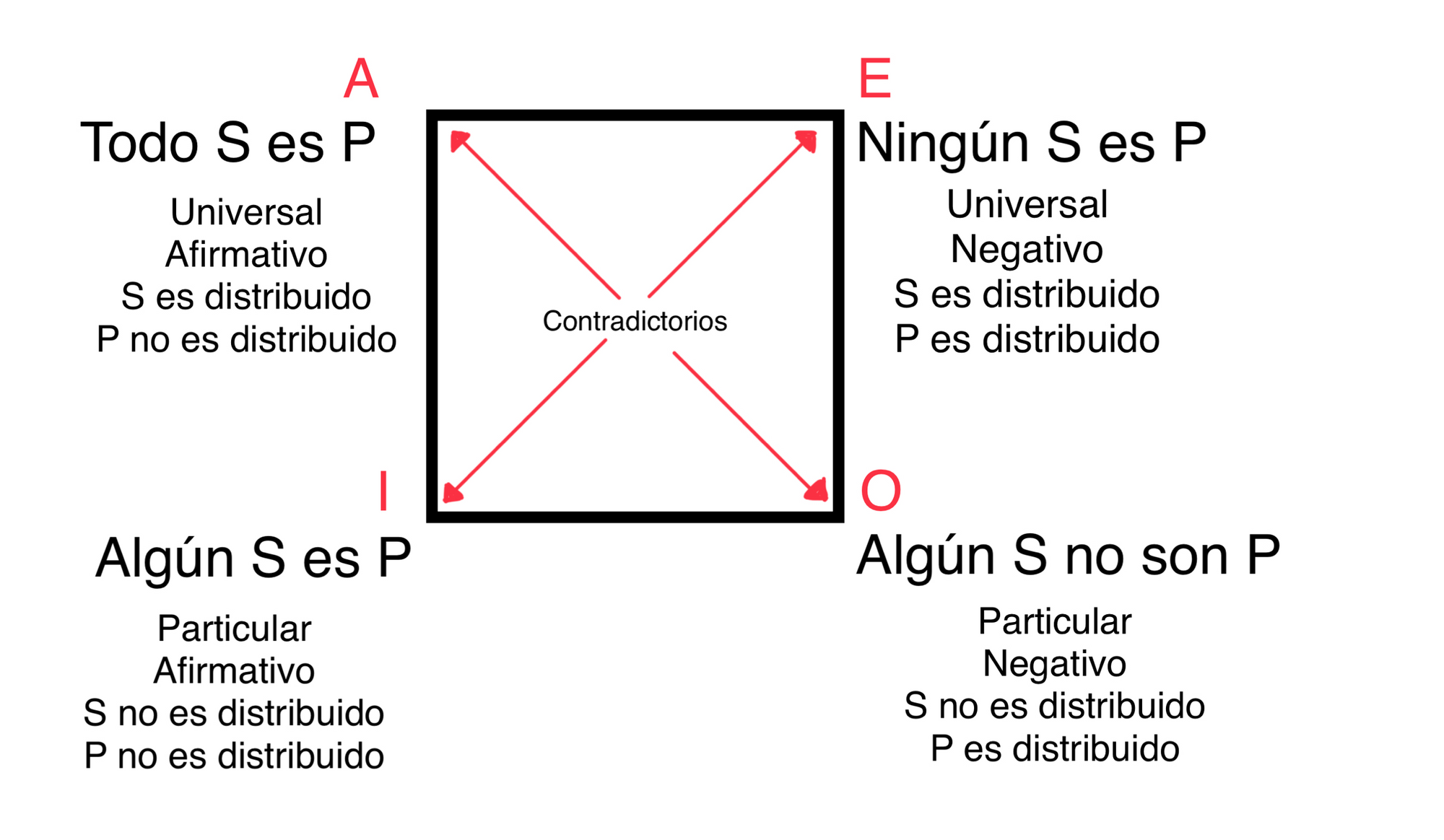
El Cuadro de Oposición es explicado en el Video enlazado arriba.
Parte 3: Visualizando la lógica categórica - diagrama ven .
Las proposiciones estándar se pueden visualizar usando el diagrama ven. Los círculos se unen y crean zonas que se designan según las proposiciones en consideración. Hagamos los diagrama para nuestras proposiciones estándar. el círculo de la izquierda representa a una clase con todos sus miembros. El Círculo del centro representa a una clase vacía, es decir es una representación de un clase sin miembros. El círculo de la derecha indica qué hay por lo menos un miembro en ese grupo. Cuando asignemos términos o proposiciones a cada círculo, esto tendrá más sentido. Veamos como funciona.

Cuando dos círculos se unen representan una proposición donde cada círculo corresponde a un termino S o P. Los círculos ahora forman un diagrama con cuatro zonas. La zona 1 representa la clase de cosas que pertenecen al termino S. La zona 2 a todo lo que pertenece a ambos términos, la zona 3 a aquello que solo pertenece a el termino P, y la zona cuatro a lo que no toma parte en la clase de términos S o P.
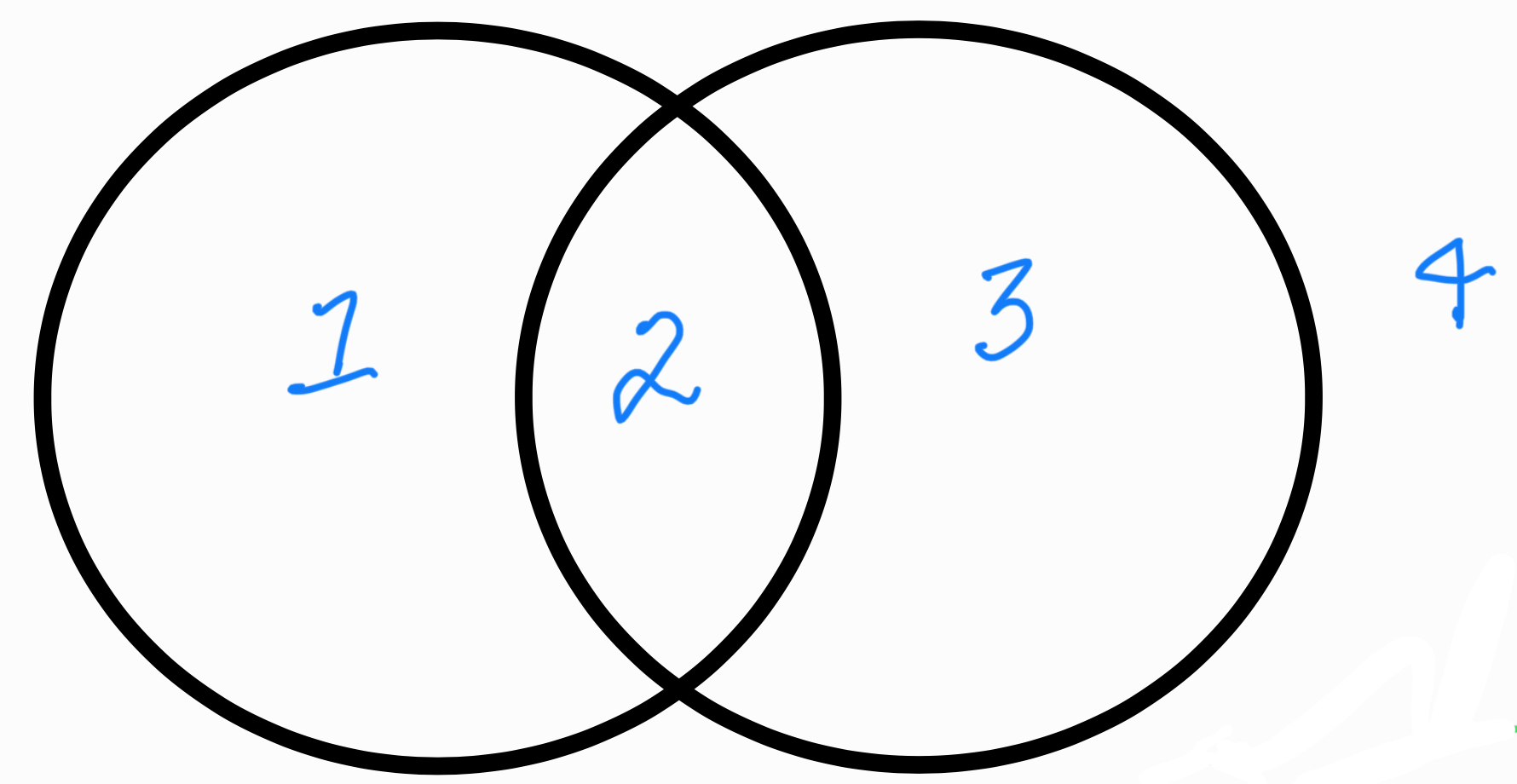
Es importante recordar done se encuentras las zonas para poder llenar la representación de la proposición correctamente. Esto será aun mas importante cuando hablemos sobre representación de silogismos.
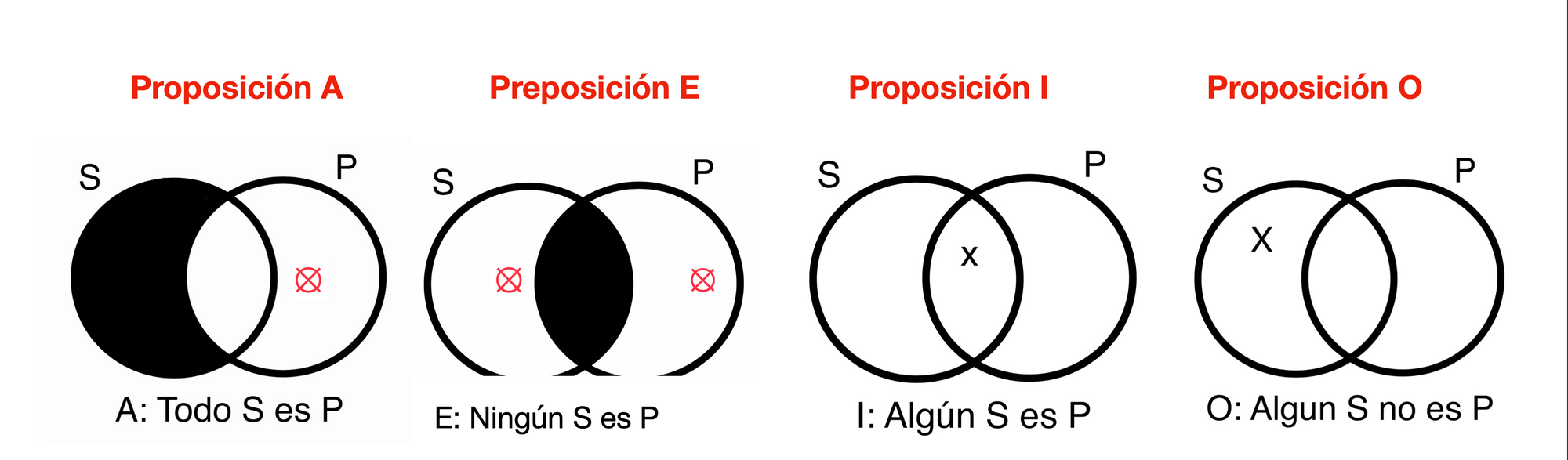
Parte 4: inferencias Inmediatas.
Un argumento inmediato (o inferencia inmediata) se refiere a una operación que se puede deducir de solamente una proposición categórica. La proposición que resulta de una operación semejante puede ser o no ser lógicamente equivalente. Aquí veremos tres diferentes argumentos inmediatos: la conversión, obversión, y contraposición lógica. Las proposiciones y sus respectivas inferencias inmediatas que resultan ser lógicamente equivalente están marcadas con un asterisco * en el texto y en amarillo en la imágenes de sus respectivos diagrama ven. Los diagrama ven confirman la equivalencia cuando el diagrama de la proposición y su inferencia inmediata son idénticos. En el caso que resulten diagramas distintos, podemos concluir que la operación no resulta en una proposición lógicamente equivalente.
Conversión
La Inferencia inmediata se lleva acabo cuando de una proposición resulta otra con los términos cambiados uno por el otro. Es decir que los términos son intercambiados, el termino S toma el lugar del predicado y el predicado toma el lugar del sujeto. Veamos la conversión de nuestras proposiciones estándar.
Declaración A: Todo S es P.--> Conversión A : Todo P es S.
*Declaración E: Ningún S es P. -->*Conversión E: Ningún P es S.
*Declaración I: Algún S es P. --> Conversión I: Algún P es S.
Declaración O: Algún S no es P. --> Conversión O: Algún P no es S.
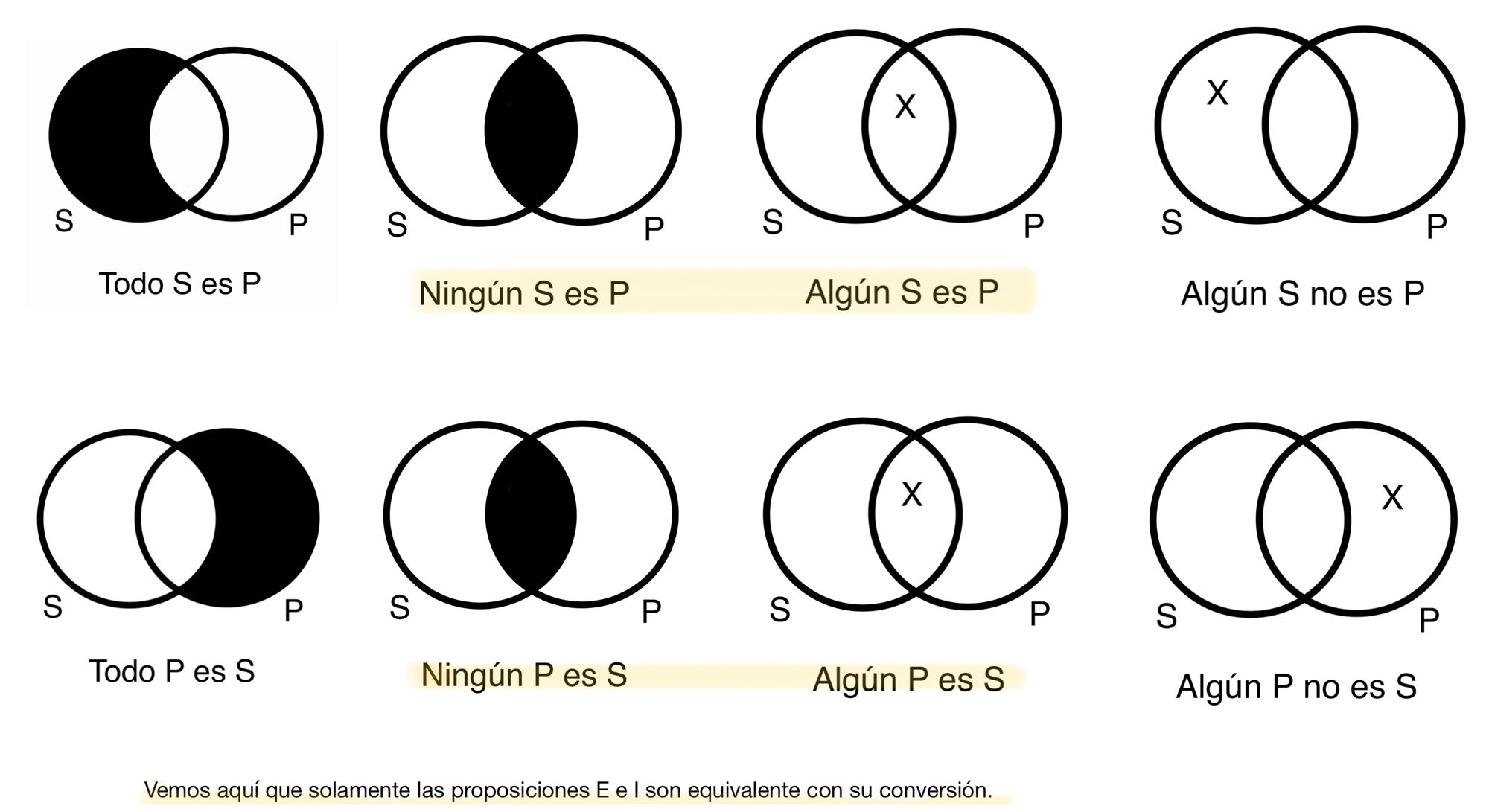
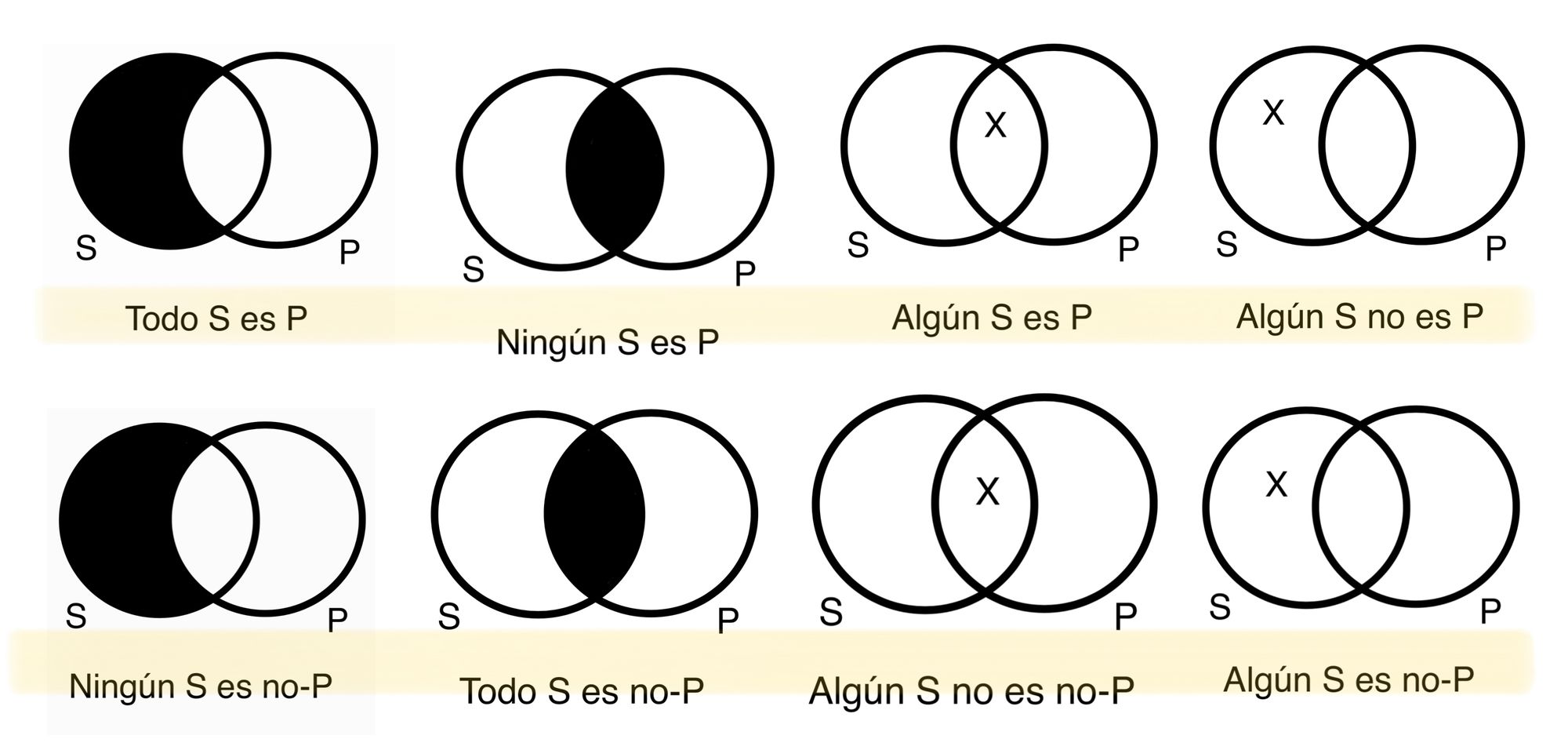
Obversión
La inferencia inmediata se lleva acabo cuando a una proposición se le aplican las dos siguientes operaciones: cambiar la calidad de la proposición y cambiar el termino que predica sobre el sujeto a su negación (no-P).
Es importante notar que la obversión de nuestras proposiciones estándar cambian una proposición a otra. Por Ejemplo, la obversión de la proposición A resulta en una proposición E.
*Declaración A: Todo S es P. --> Obversión E: Ningún S es no-P.
*Declaración E: Ningún S es P --> Obversión A: Todo S es no-P.
*Declaración I: Algún S es P. --> Obversión O: Algún S no es no-P
*Declaración O: Algún S no es P. --> Obversión I: Algún S es no-P.
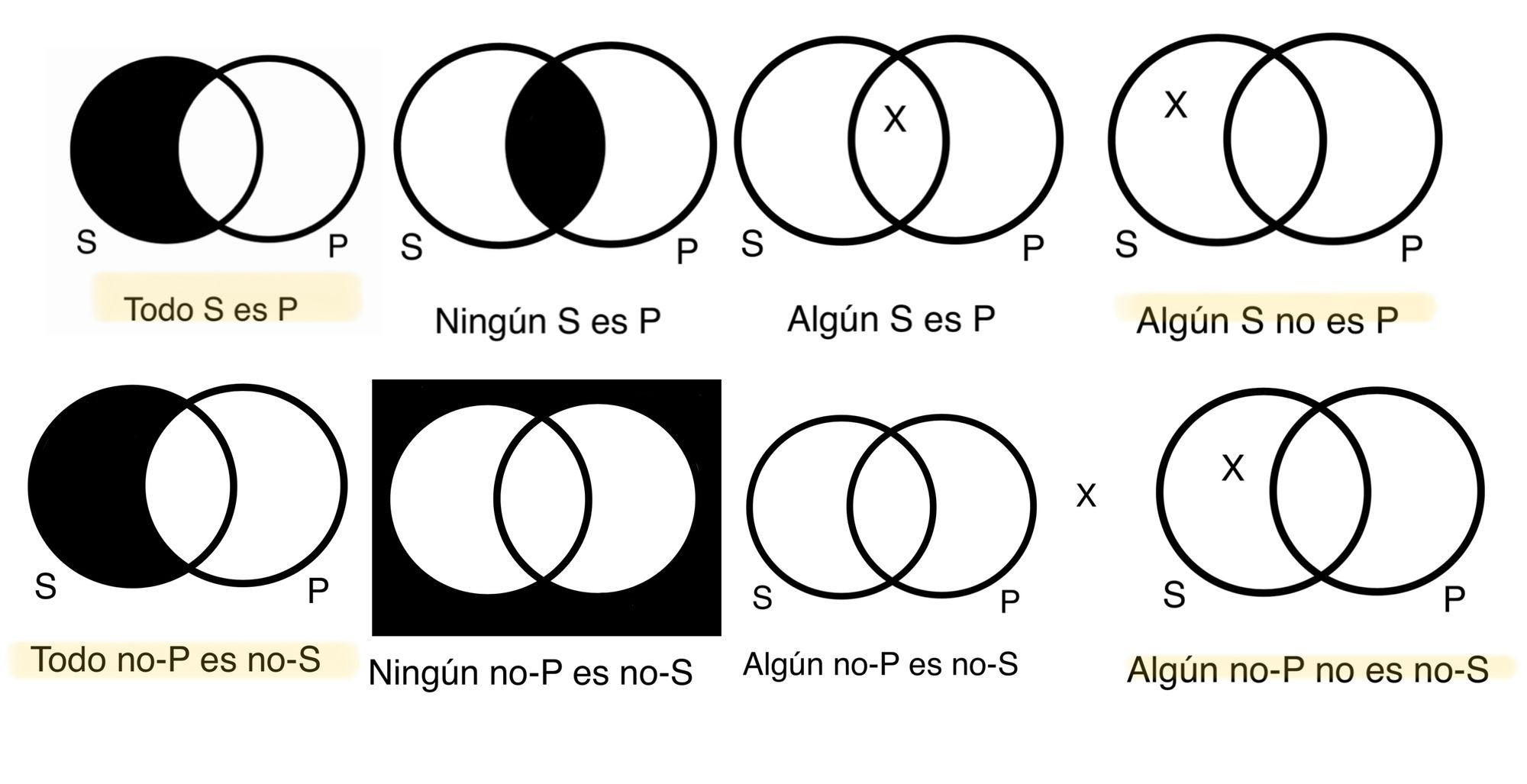
Contraposición
La inferencia inmediata se lleva acabo cuando a la proposición declarada se le aplican las siguientes operaciones: Cambiar la posición de los términos uno por otro y cambiar ambos también por su complemento (no-S y no-P).
*Declaración A: Todo S es P. --> Contrarrecíproco A: Todo no-P es no-S
Declaración E: Ningún S es P --> Contrarrecíproco E: Ningún no-P es no-S.
Declaración I: Algún S es P. --> Contrarrecíproco I: Algún no-P es no-S.
*Declaración O: Algún S no es P --> Contrarrecíproco O: Algún no-P es no-S.
En Práctica!
La inferencia inmediata se utiliza, entre otras cosas, para traducir oraciones en lengua común a una de las proposiciones estándar.
Veamos algunos ejemplos.
Algunos negocios son desorganizados.
Podemos ver que esta declaración es una forma de proposición I: Algún S es P (la copula es la conjugación del verbo ser).
Algunos negocios son desorganizados.
Si el problema no es evidente los inferencia inmediatos nos serán aquí util. La conversion de la proposición I es lógicamente equivalente y por lo tanto beberíamos poder aplicar la conversión. Aplicando la inferencia vemos inmediatamente el problema:
Algunos desorganizados son negocios.
Notemos que las proposiciones categóricas usan términos que representan clases de cosas y los adjetivos no son clases de cosas. En este caso, debemos remplazar el adjetivo con un nombre. Podríamos usar organizaciones desorganizadas en lugar de el adjetivo "desorganizadas" y después substituir los nombres por términos como en las proposiciones estándar:
Algunas (O) organizaciones desorganizadas son (N) negocios.
y resulta una proposición estándar:
Algún O son N. ( Algún P es S).
Si aplicamos la inferencia de nuevo tendremos nuestra proposición original en una traducción aceptable.
Algún N es P. o Algún S es P.
Veamos otros ejemplo.
Si una persona tiene 100 dólares no es rica.
Aquí vemos la necesidad de tratar con la forma condicional del lenguaje. En este caso será necesario identificar la cantidad correctamente. Esta frase se refiere a todas las personas que tengan el monto de dinero de 100 dólares. Tendremos una proposición universal. Ahora solo queda determinar la calidad. La calidad se determina por la copula que en este caso es negativa.
Si alguien es "persona con $100" esa persona es "no-persona rica."
esta proposición es equivalente a una proposición estándar A:
toda P (persona con 100 dólares) es no-R (persona rica).
Pero esta frase se puede simplificar aun mas por que la obversion de una proposicion A es una Proposicion E. La obversion (los pasos de la inferencia obversion esta descritos en esta sección) nos resulta con la siguiente proposición :
Ningún P (persona con $100) es R (persona rica).
Una proposición universal y negativa como nuestra frase en lengua común original.
Parte 5: Silogismos Categóricos
El silogismo categórico: es un racionamiento deductivo compuesto de tres proposiciones categóricas—dos proposiciones como premisas y una como conclusión. La conclusión, si el argumento es valido, se puede deducir de la misma manera y con la misma certeza que la proposición aritmética "2+2=4." La validez lógica es característica de un argumento del cual la conclusion es implicada por las premisas. En el silogismo categórico los términos S y P ahora sirven un nuevo propósito. Para entender el silogismo hay que incorporar nuevos terminos a nuestro vocabulario. Bienvenidos a la argumentación.
Termino Mayor: El termino predicado de la conclusión. Este termino ocurre una vez con el termino medio en la premisa mayor.
Termino Menor: El termino sujeto de la conclusión. Este termino ocurre una vez con el termino medio en la premisa menor.
Termino Medio: El Termino que no ocurre en la conclusión de un silogismo.
Premisa Mayor: La primera premisa del silogismo que contiene el termino mayor.
Premisa Menor: La segunda premisa del silogismo que contiene el termino menor.
Conclusión: La proposición implicada por las premisas. Esta proposición no contiene el termino medio.
Un silogismo con forma estándar sigue las siguientes reglas:
- Todas las proposición en si deberán estar en una de las cuatro forma estándar (A, E, I , O), aplicando las inferencias inmediatas cuado sea necesario.
- Cada termino aparecerá dos veces de una manera idéntica y con el mismo significado. Se considera falacia cambiar el significado de un termino dentro del silogismo.
- Las premisas aparecerán en la siguiente orden: premisa mayor—>menor—> conclusión.
Por ejemplo:
Todo Hombre es Mortal.
Socrates es un Hombre.
________________(línea denota una conclusión)
Socrates es Mortal.
Este ejemplo famaso sigue las tres reglas? No como esta escrito. Recordemos que las proposiciones deben de presentar se en forma estándar y a veces es necesario traducir oraciones en lengua común a proposiciones categóricas.
El Termino Medio del silogismo es Hombre (H).
La Premisa Mayor: Todo Hombre es Mortal se puede traducir a
Todo H es M.
La Premisa Menor: se tendrá que traducir a una proposición estándar.
Los terminos dentro de propocisiones deberian de representar a una clase de cosas. En el caso de un nombre personal, como Socrates, lo que se debe entender es que existe una clase de cosas que se llama Socrates que contiene solamente un miembro, y ese miembro es Socrates mismo. La proposición que resulta de esta formulación es la siguiente:
Toda Persona idéntica a Socrates es Hombre. Esta proposicion se presenta asi:
Todo P (personas idénticas a Socrates) es H.
La conclusion: Socrates es Mortal se puede traducir a
Todo P es M.
El silogismo categorico que resulta de nuestro ejemplo es
Todo H es M.
Todo P es H.
__________
Todo P es M.
La siguiente pregunta es, ¿es valido el argumento? Para determinar la validez hay que entender mejor el silogismo y utilizar el diagrama ven para confirmar nuestras conclusiones.
Animo y Figura del Silogismo Categórico.
El animo de un silogismo categórico se determina por el typo y orden de las proposiciones estándar que contiene el silogismo. En un silogismo estándar hay tres proposiciones y pueden ser cualquier combinación de las proposiciones A, E, I u, O. En el ejemplo de Socrates el animo es AAA porque las tres proposiciones estándar son typo A. En otro caso: si la premisa mayor es una proposición A , la premisa menor E, y la conclusión I, el animo del silogismo sería a AEI.
La figura del silogismo se determina por el orden del termino medio en las premisas del argumento. Hay cuatro posibilidades.
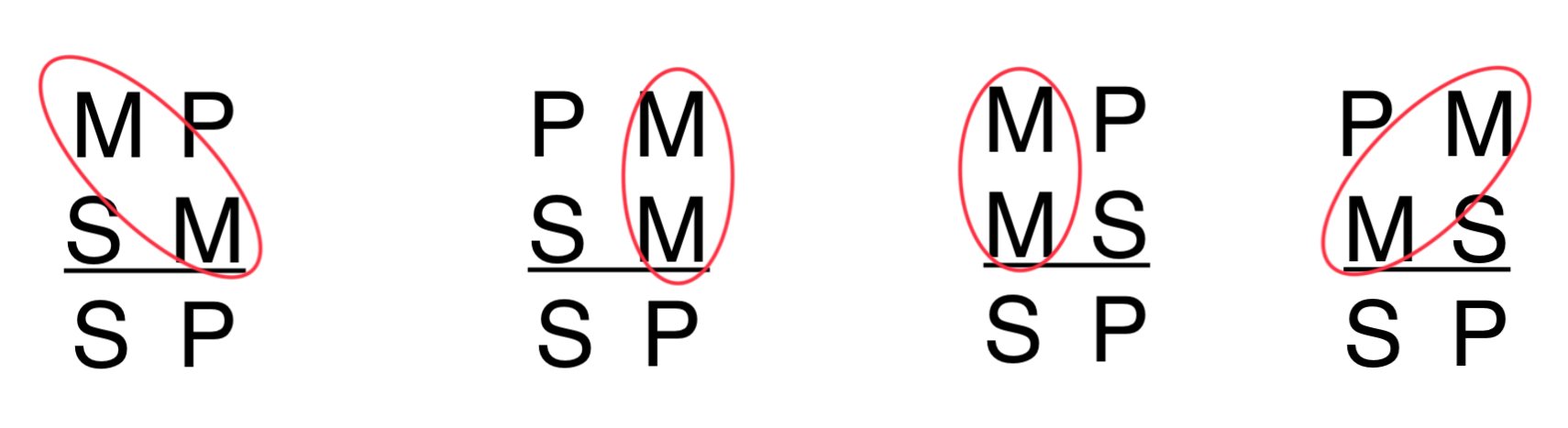
La figura del ejemplo de Socrates es 1, ya que el termino medio en ese ejemplo (H) aparece como sujeto en la premisa mayor y como predicado en la premisa menor.
La lógica categórica reconoce 256 combinaciones de silogismos con animo y figura pero solamente 15 que tienen validez lógica en la interpretación tradicional y moderna. Aquí las 15.
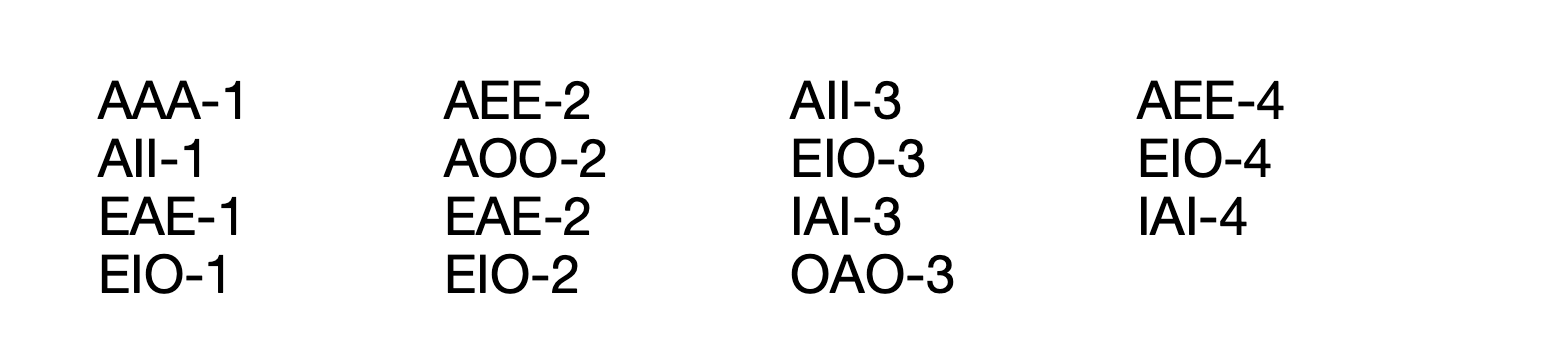
Seria ideal recordar estas 15 formulaciones, pero quiza no es lo mas practico. Por eso, es importante saber utilizar los diagrama ven para verificar la validez de un silogismo. En la siguiente sub-sección haremos exactamente eso con varios silogismos validos en esta lista.
Hemos visto que el diagrama ven proporciona un circulo representando a cada termino de una proposición. En el caso del silogismo, que contiene tres términos, contiene también 3 círculos. Aquí esta el diagrama con sus respectivas zonas.
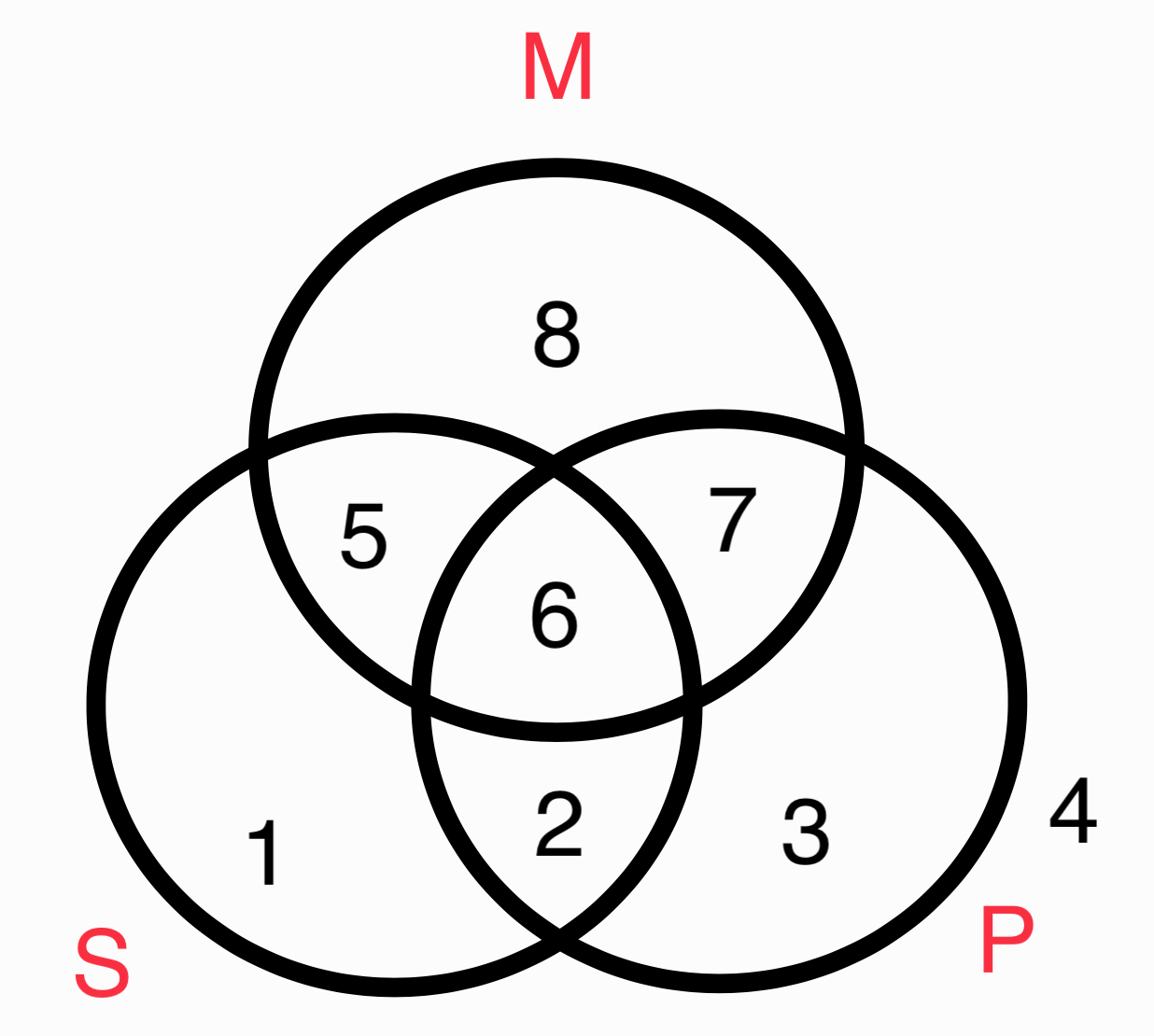
Diagramando silogismos categóricos.
Ilustrando un silogismo no implica algo diferente de lo que ya fue establecido. Es solo qué hay que ilustrar las premisas en orden comenzando con la premisa universal y después lo que resta. No es necesario ilustrar la conclusión de un silogismo ya que la conclusión es el resultado de las premisas mayor y menor y al ilustrar estas la conclusión resulta deductivamente. Tomemos un ejemplo:

En este caso proseguimos utilizando letras mayúsculas para representar los términos S, P, y M.
Frutas = F, cosas dulces = D, manzanas = M. El siguiente silogismo resulta:

Luego será necesario diagramar las premisas. Comenzamos con la premisa mayor (imagen titulada premisa mayor) luego la menor (imagen titulada premisa menor) y finalmente ambas juntas (titulada conclusion).
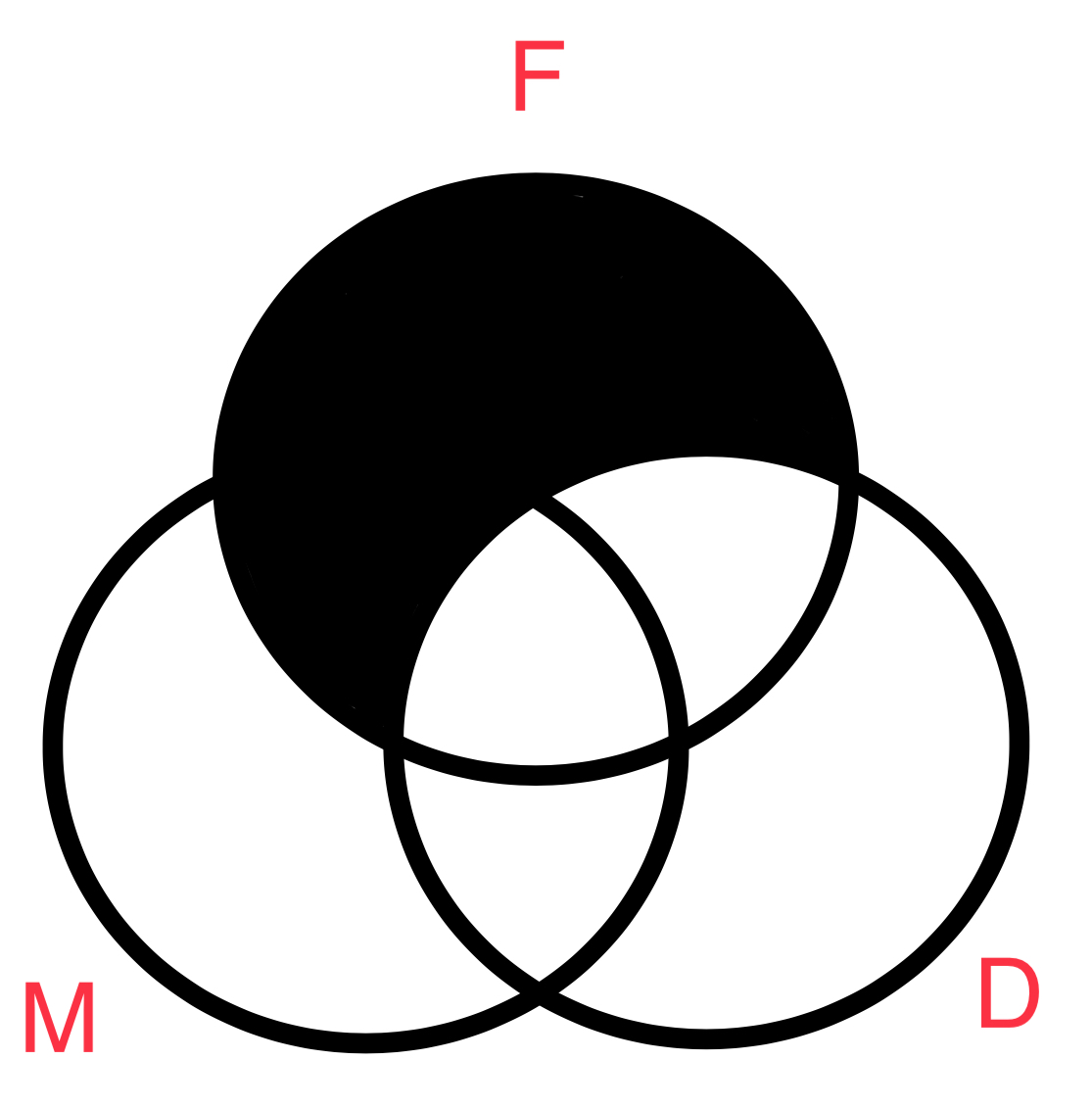
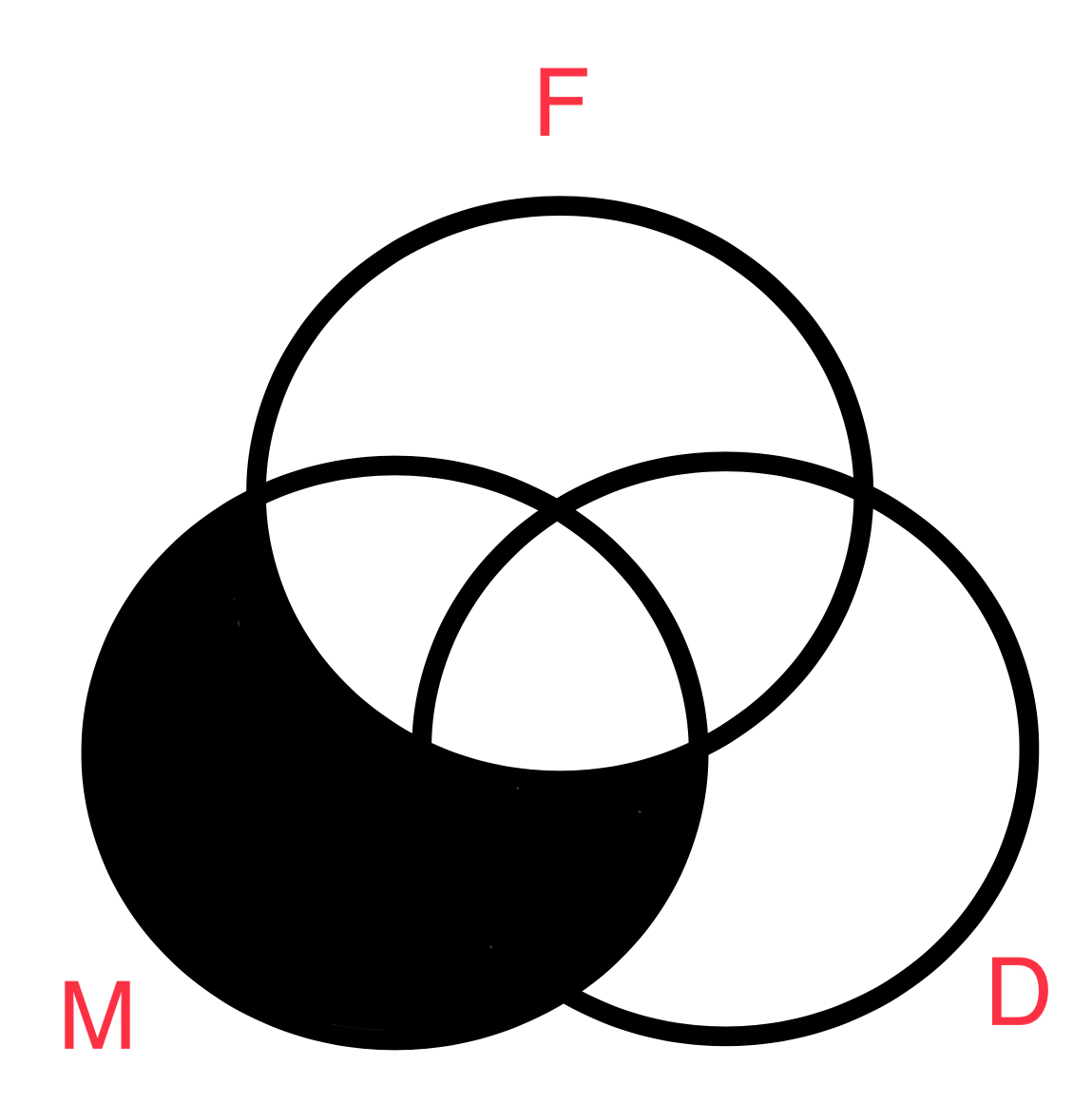
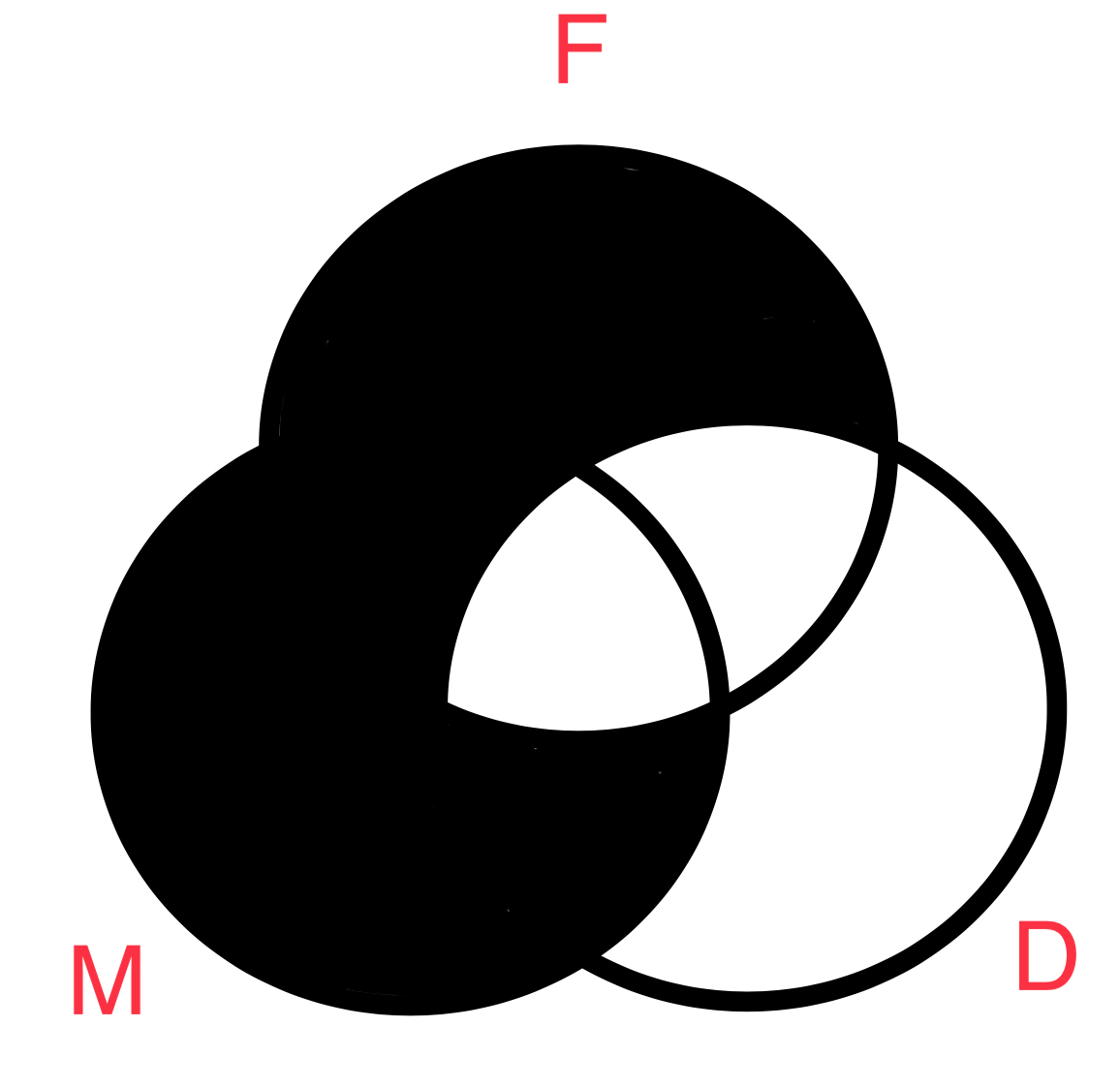
Lo importante a notar es que la imagen de la conclusión representa la union del diagrama de las premisas mayor y menor. De esta forma el diagrama ven nos permite verificar validez logica. Otra manera de confirmar la validez es haciendo referencia al animo y la figura del argumento. En este caso, como lo hizo el diagrama, su forma y figura (AAA-1 ) lo confirman también. El diagrama nos confirma lo que nuestra interpretación moderna nos afirma, si algo es M también es D. O en lenguaje común, todas las manzanas son cosas dulces. Podemos visualizar que nuestro argumento es valido. Veamos aun otro ejemplo.
Un silogismo de forma y animo de EIO-3 es valido y el diagrama no lo confirmará.

Establecemos los terminos para crear un silogismo categorico con propocisiones estandar: Fruta = F, cosa amarga= A, manzana = M

Después utilizamos los diagramas para cada premisa y la conclusión.
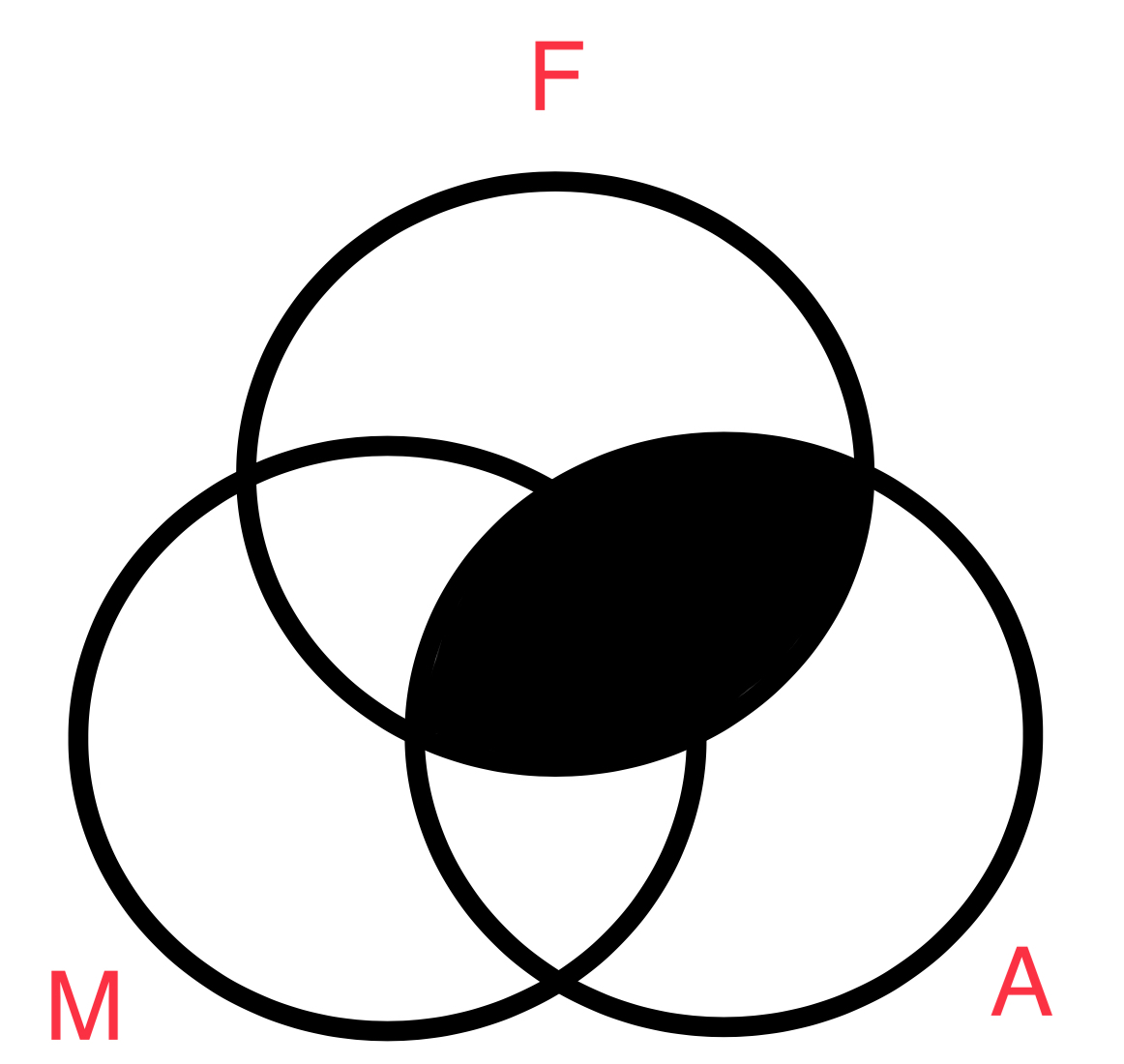
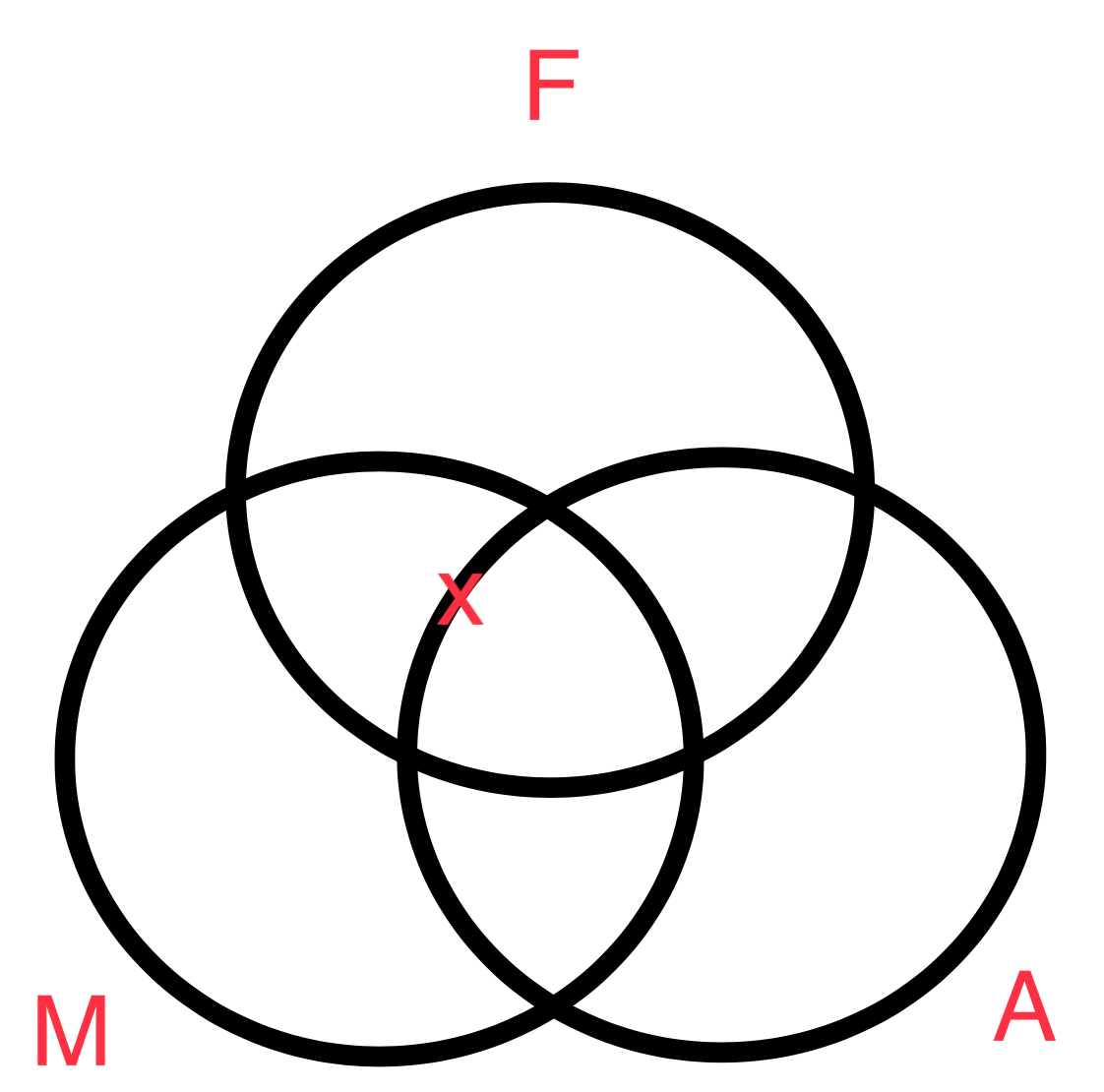
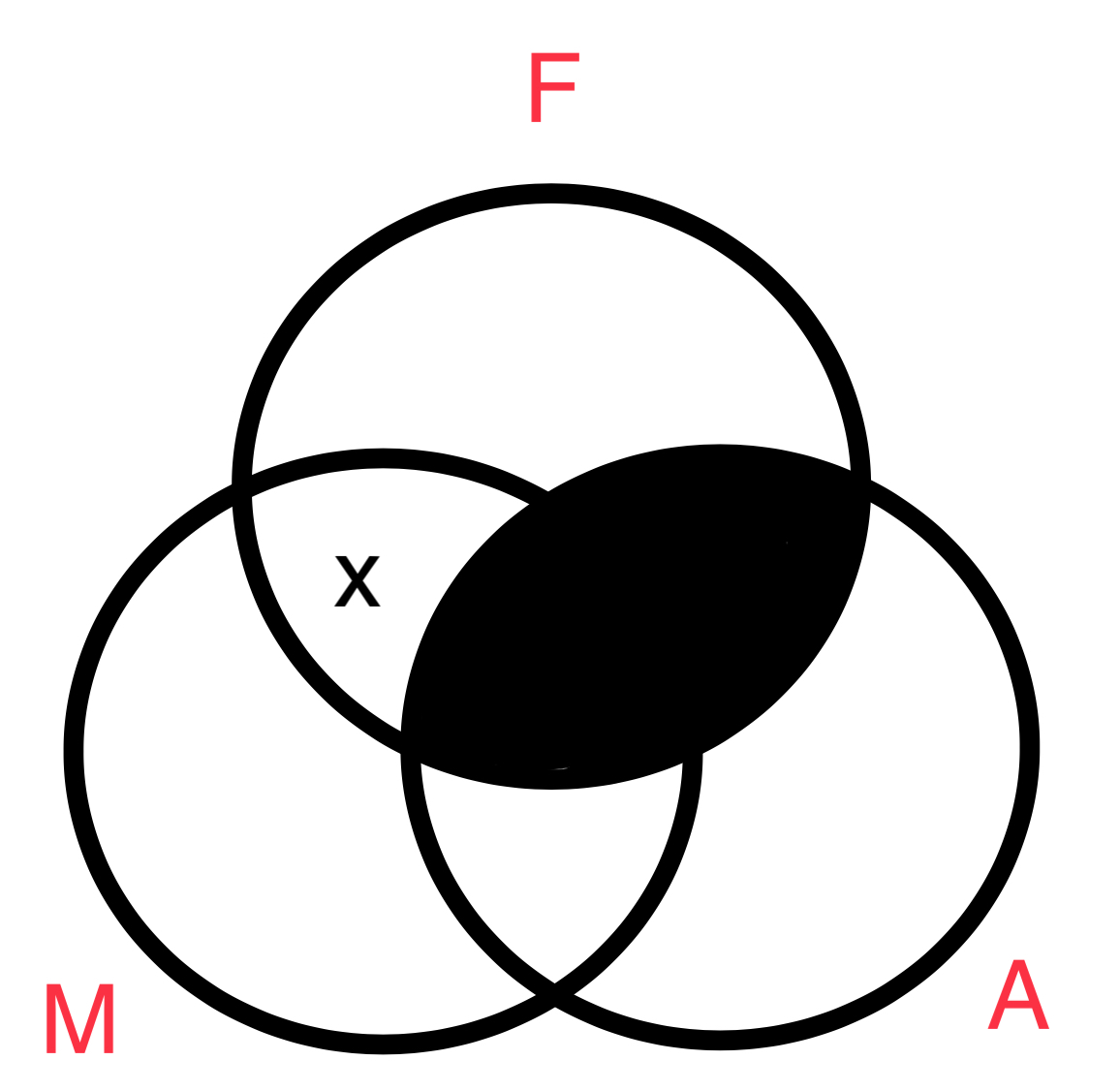
El diagrama de la conclusión es exactamente la union de las premisas. Lo importante a notar es la pocision de la "X." Cuando se diagrama la premisa menor la "X" se encuntra entre la zona 5 & 6. Esto es porque la premisa en si no da suficiente informacion sobre el miembro de la clase. Solamente nos afirma que hay por lo menos un M que es tambien F, pero no si tambien es A. Cuando se diagraman varias premisas juntas, como en la conclusion, que es la union de dos premisas, se comienza con la propocisión universal. Y por lo tanto, en nuestro ejemplo comenzamos con la premisa mayor la cual deja la zone 6 vacia (representada por el relleno de color solido). Esto aclara que la "X" de la premisa menor no puede pertenecer a la zona 6 por que esta zona esta vacia. En fin, el silogismo categorico es valido y su figura y su forma y figura es EIO-3.
Veamos un ejemplo que resulta ser invalido. Este tendrá la forma de EAA-1

En este caso proseguimos utilizando letras mayúsculas para representar los términos S, P, y M.
Frutas = F, cosas dulces = D, manzanas = M. El siguiente silogismo resulta:

Luego diagramamos la premisa mayor:
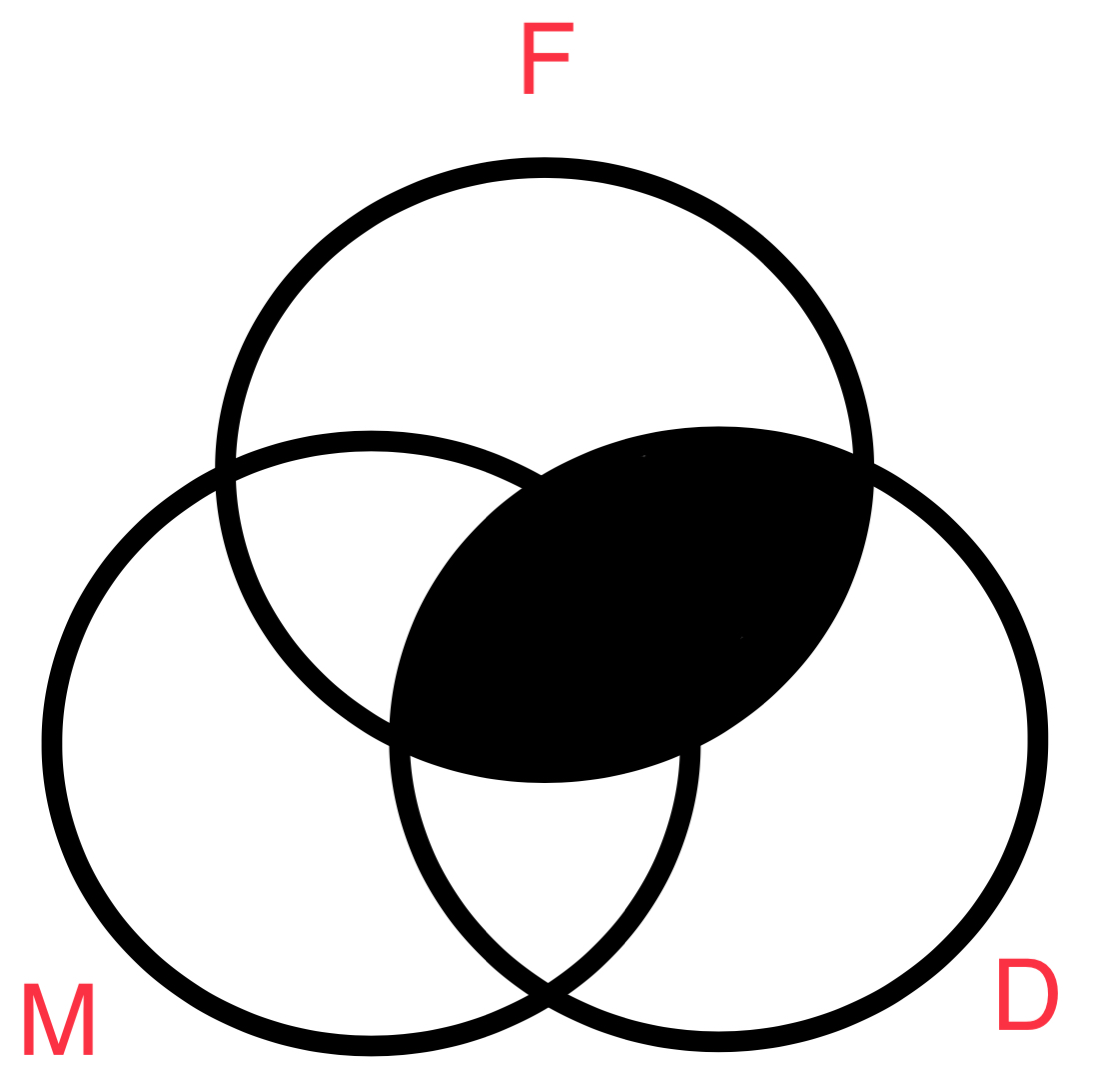
La premisa menor:
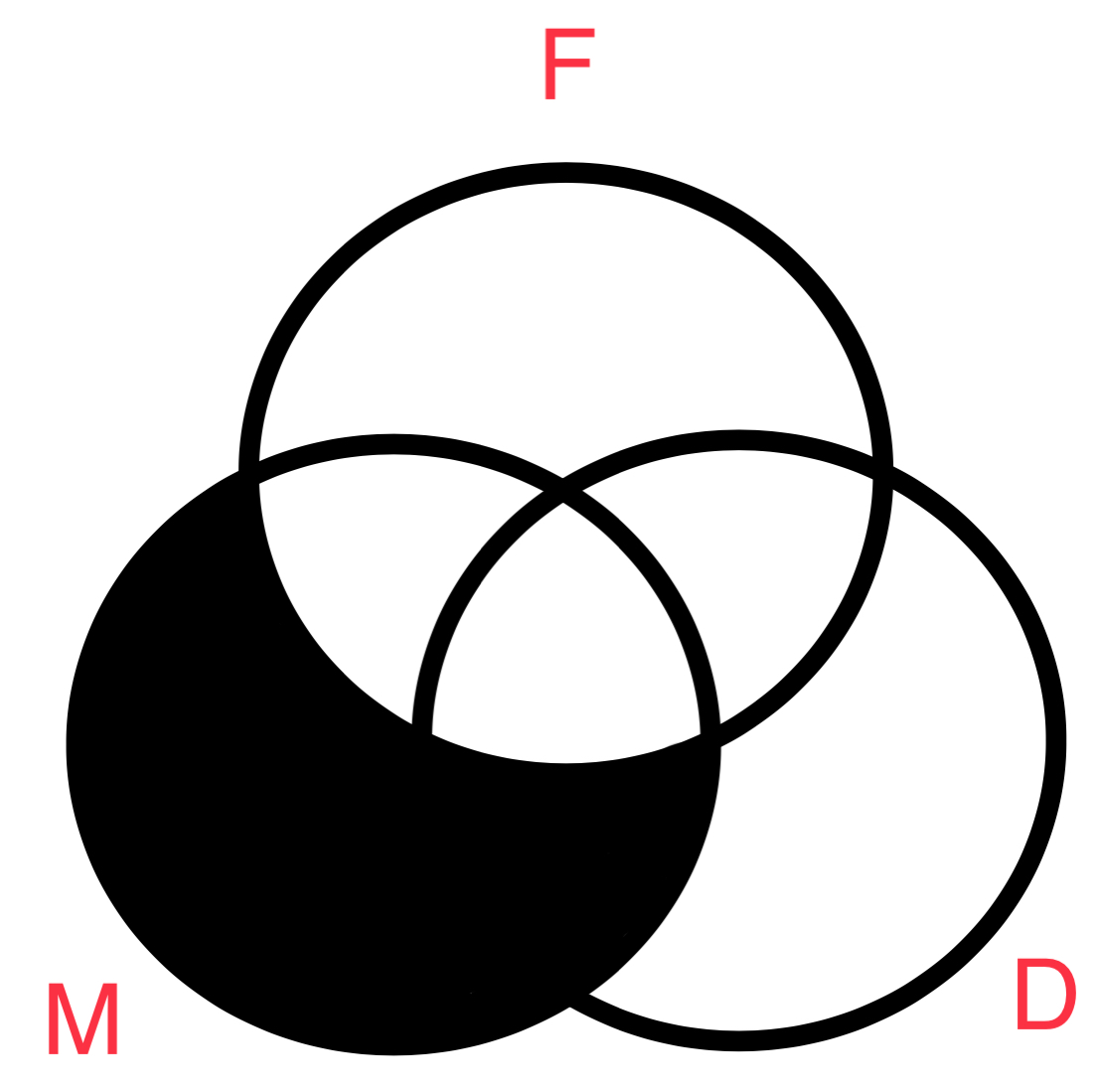
Y la conclusión:
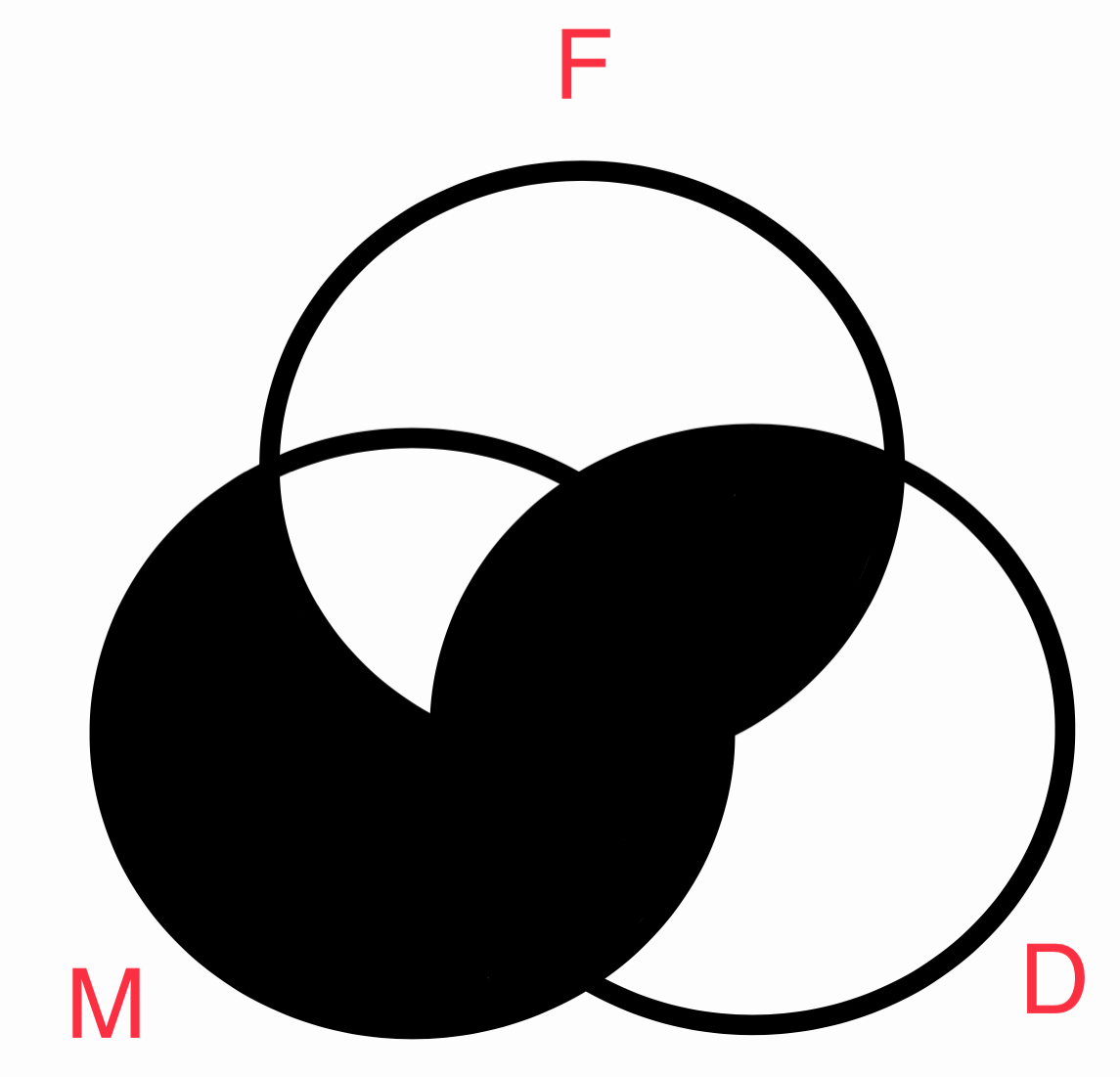
El diagrama ven nos confirma que este argumento es invalido. Lo sabíamos por que conocemos todos los argumentos que son validos, hay 15. También sabemos que es invalido por que esta en violación de la reglas y falacias (#4) de la lógica categórica que nombraremos en un momento. Antes, notemos que el diagrama de la conclusión excluye la posibilidad de que algún M sea también D. Y por lo tanto concluimos que ningún M es D es la conclusión valida y no Todo M es D por que las zonas 2 & 6 están vacías. No hay ningún M que también sea D en este diagrama.
Parte 6: las reglas según la interpretación moderna sobre silogismos categóricos.
Regla #1: el termino medio (M) debe ser distribuido en por lo menos una premisa.
Regla #2: si un termino, ya sea S o P, es distribuido en la conclusión, tendrá que ser también distribuido en la premisa.
Regla #3: un silogismo categórico no puede tener dos premisas negativas.
Regla #4: si el silogismo contiene una premisa negativa, la conclusión será negativa.
Regla #5: si la conclusión es negativa, el silogismo tendrá una premisa negativa.
Regla #6: dos premisas universales no pueden tener conclusión particular.
Este es el final del curso, espero y lo disfrutaron. Las partes principales de este curso estan en produccion y seran publicadas en su momento. Esten pendientes y gracias. Este curso debería ser solamente una introducción a la lógica categórica y sus limitaciones son simplemente resultado de ese echo. Cualquier duda o comentario, favor de dejar un comentario ó comunicarse con el autor Omar Moreno escribiendo a omoreno@conservamus.com De nuevo, gracias.
Member discussion